Metric Learning: Part 1

Note: this post is the first part of the distance metric series. The first post discusses “Distance Metric Learning, with application
to clustering with side-information” (http://ai.stanford.edu/~ang/papers/nips02-metric.pdf) and the
second post discusses “Geometric Mean Metric Learning” (http://suvrit.de/papers/GMML.pdf)

I attended one of the optimization session on the first day of ICML and one of the talks I listened to was about geometric
mean metric learning (http://suvrit.de/papers/GMML.pdf). I was amazed by their result so I’ll make some notes about
their method for myself.

In many machine learning tasks (i.e. classification, search, clustering),
it is necessary to learn some sort of notion of distance between input
data points. For example, in classification, one needs to –

Metric learning was (first?) introduced in this paper: “Distance Metric Learning, with application
to clustering with side-information”
http://ai.stanford.edu/~ang/papers/nips02-metric.pdf.

Problem Setting

Suppose we have a set of points $\{x_i\}_{i=1}^n \subseteq R^m$. Suppose also we are given a set of “side information” that tells us that a certain set of points are “similar” s.t. $S: (x_i, x_j) \in S \text{ if } x_i \text{ and } x_j \text{ are similar. }$ How can we encode this similar-dissimilar information in a distance metric?

Simple answer

Learn a Mahalanobis distance $d(x,y) = \sqrt{(x-y)^T A (x-y)}$ so that $A$ will somehow encode the desired information.

Now the problem is reduced to how to learn the matrix A. Whenever we want to learn something, we should remind ourselves of viewing it as optimization. To do so, we need to define what we want to minimize (or maximize…just flip the sign of the objective function), which should correspond to the notion of “goodness” of the matrix A. But before that, we will go over how the Mahalanobis distance came in.

Mahalanobis distance in R^2

To get the feel of it, we will look at some examples.

1
2
3

import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

%matplotlib inline
mu = [0, 0]
cov = [[1,0],[0,1]]
x_data, y_data = np.random.multivariate_normal(mu,cov,500).T
#x_data = np.float32(np.random.rand(1,1000))
#y_data = np.float32(np.random.rand(1,1000))
fig = plt.figure(figsize=(8,8))
plt.axis([-10.0,10.0,-10.0,10.0],size=20)
plt.grid(True)
ax = fig.add_subplot(1,1,1)
plot_out = plt.scatter(x_data,y_data,color='b',marker='o',label="$K_2,mu_2$", alpha=0.3)
circle = plt.Circle((0,0),1,color='r', fill=False, alpha=0.9)
plot_out = ax.add_artist(circle)
#plot_out = plt.plot(x_data, y_data, "bo", alpha=0.3, )
#plt.show()

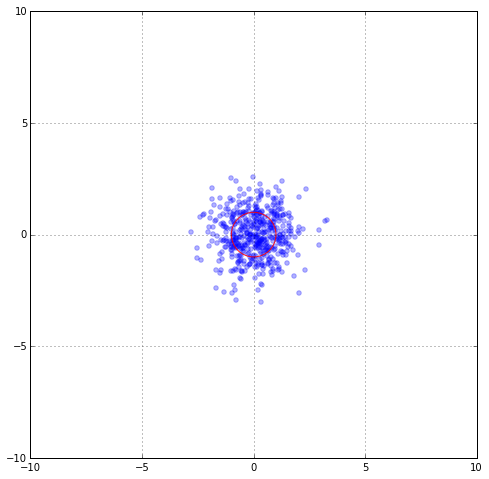
Suppose that the data distribution were Gaussian and our data samples are distributed according to $N(0, I)$. The red circle marks the unit standard deviation. Now, take two blue points x and y. The Euclidian distance between x and y is $|| x - y ||_2 = \sqrt{(x-y)^T (x-y)}$. Now normally the data are not distributed according to Gaussian, but rather some obscure distribution. In this data distribution, some data samples might be “similar” and others are not. If we use Euclidian distance as a way to measure similarity, we might end up disregarding the intrinsic information within the data distribution. We want to “correct” this.

To be more concrete, suppose our real data distribution were something like $\mu = 0$ and $Cov = [[1,0], [0, 6]], which is still too simplistic for any real data. Then sample distribution might look like this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

%matplotlib inline
mu = [0, 0]
cov = [[3,1],[1,2]]
x_data, y_data = np.random.multivariate_normal(mu,cov,500).T
#x_data = np.float32(np.random.rand(1,1000))
#y_data = np.float32(np.random.rand(1,1000))
fig = plt.figure(figsize=(8,8))
plt.axis([-10.0,10.0,-10.0,10.0],size=20)
plt.grid(True)
ax = fig.add_subplot(1,1,1)
plot_out = plt.scatter(x_data,y_data,color='b',marker='o',label="$K_2,mu_2$", alpha=0.3)
circle = plt.Circle((0,0),1,color='r', fill=False, alpha=0.9)
plot_out = ax.add_artist(circle)
# TO DO: I should fix the red circle so that it will correspond to the blue distribution.

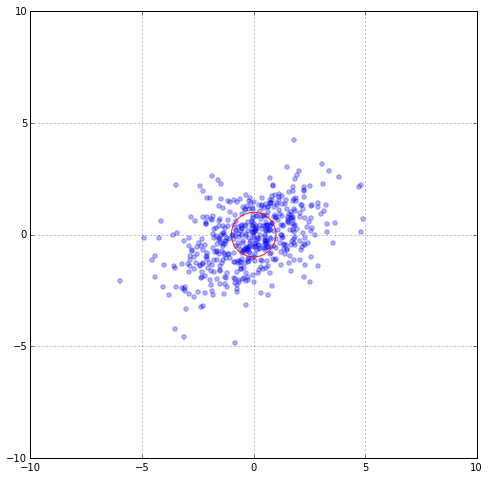
In order to reflect the distortion, we should use ; what is the correct way to measure the distance between x and y in the new plot? For example, can we say that the point at the top of the distribution and that point right this and this are the same distance? We should fix this because we think that those two points that are along the principle direction should be “more” similar than those that are not (in this case perpendicular). How can we fix this? By rotating back. The rotation matrix we used was C. So one correct distance metric we could use is $|| x - y ||_{C^{-1}} = \sqrt{(x-y)^T C^{-1} (x-y)}$

Now let’s go back to the paper. What the paper says is this: why not let the data decide which matrix $C^{-1}$ to use.

Optimization problem

The simplest formulation would be : $\min \sum_{x_i, y_i \in S} || x_i - y_i ||_A$. However, this would lead to the non-interesting answer which is to let A be 0 matrix, which will give us 0 for even pairs of x and y which are in a dissimilar set $D$. So we should have a restriction which prevents that to happen. One way to do is add a constraint on $A$ such that $\sum_{x_i, y_i \in D} || x_i - y_i ||_A \ge c$, where $c$ is some positive constant. such that (most of) $|| x_i - y_i ||_A = 0$ even if $x_i \neq y_i$, which is not even a distance anymore. (Recall the definition of “distance”.) So the final form is:
$\min \sum_{x_i, y_i \in S} || x_i - y_i ||_A \text{ s.t. } \sum_{x_i, y_i \in D} || x_i - y_i ||_A \ge c \text{ and } A \succeq 0$

Notes for myself: Ch19 Approximate Inference http://www.deeplearningbook.org/contents/inference.html

Introduction

• Inference = compute $P(h|v)$.

• There are many situations where you want to calculate the posterior distribution $P(h|v)$ (i.e. sparse coding, ). Here, h is a set of hidden variables and v is a set of observed variables. In general, when the model is complicated, it is intractable to compute the corresponding $P(h|v)$. This chapter introduces many examples of the inference problem, which approximates $P(h|v)$.

19.1 Inference as Optimization

• The core idea of approximate inference.

• Given a probabilistic model with latent variables $h$ and observed variables $v$, we want to know how good it is. One measure of goodness is $\log p(v; \theta)$, often called model evidence or marginalized likelihood.

• When integrating out $h$ is difficult, we instead seek for an alternative. Is there a way to lower bound $\log p(v, \theta)$?

• Consider the following:
  $$
  L(v, \theta, q) = \log p(v; \theta) - KL(q(h|v), p(h|v; \theta))
  $$

• Since KL divergence is always non-negative, we can think of L(v, \theta, q) as a lower bound approximation of $\log p(v, \theta)$.

• By modifying the above equation, we have

  $$L(v,\theta,q) = \log p(v;\theta) - E_{h \sim q}\log \frac{q(h|v)}{p(h|v;\theta)} \\ = \log p(v; \theta) - E_{h \sim q}\log\frac{q(h|v)}{\frac{p(v,h; \theta)}{p(v; \theta)}} \\ = \log p(v; \theta) - E_{h\sim q}[ \log q(h|v) - \log \frac{p(v,h; \theta)}{p(v; \theta)}] \\ = - E_{h\sim q}[ \log q(h|v) - \log p(v,h; \theta)] \\ = - E_{h\sim q}[ \log q(h|v)] + E_{h \sim q}[\log p(v,h; \theta)] \\ = E_{h \sim q}[\log p(v,h; \theta)] + H(q)$$

  where $H(q) = - E_{h\sim q}[ \log q(h|v)]$.

• For an appropriate choice of $q$, $L$ is tractable.

• The following sections will show how to derive different forms of approximate inference by using approximate optimization to find $q$.

19.2 Expectation Minimization

(I thought it’s easier to view this section through an example so I’ll add some Mixture-of-Gaussian taste in my notes)

• The goal is to maximize the lower bound $L(v,\theta, q)$. Note that we have two distinct terms when we expand $L$ in the above section: the left term is parameterized by $\theta$ and the right term is parameterized by $q$.

19.3 MAP Inference and Sparse Coding

(will skip this for the time being)

19.4 Variational Inference and learning

• The core idea: maximize $L$ over a restricted family of distributions $q$.

19.5 Learned Approximate Inference

• The core idea: we can view the iterative optimization of maximizing $L(v,q)$ w.r.t. $q$ as a function $f$ that maps an input $v$ to an approximate distribution $q* = argmax_q L(v,q)$. Once we view this way, we can learn a function $f(v; \theta)$ with neural network.

Ch14 : Autoencoders

14.4 Stochastic Encoders and Decoders

Ch3 : Probability and Information Theory

http://www.deeplearningbook.org/contents/prob.html

3.13 Information Theory

Shannon entropy = $H(x)$ = $-E_{x \sim P}[\log P(x)]$ (also denoted $H(P)$)

In words, the Shannon entropy of a distribution $P$ is the expected amount of information in an event drawn from that distribution.

KL divergence = $D{KL}[P || Q]$ = $E{x \sim P}[\log P(x) - \log Q(x)]$

Cross entropy = $H(P,Q)$ = $H(P) + D{KL}(P||Q)$ = $-E{x \sim P}\log Q(x)$

Minimizing the cross-entropy w.r.t Q is equivalent to minimizing the KL divergence.

Ch5 : Machine Learning Basics

5.5 Maximum Likelihood estimation

-

• CG solves a linear equation $Ax = b$.

Derivation:

1. Recall the step size calculation of Steepest Gradient Descent.

Recall that $f(x) = \frac{1}{2} x^T A x - b^Tx + c$ is the corresponding parabollic function for the linear equation $Ax = b$ (the minus sign for b is just to make it nice when we consider the relation between $Ax=b$ and its quadratic form). And $f’(x) = \frac{1}{2}A^Tx + \frac{1}{2}Ax - b$

When $A$ is symmetric, this becomes $f’(x) = Ax - b$. So $-f’(x_i) = r_i$, where $r_i = b - Ax_i$ (residual vector)

1. Recall the typical trajectory of Steepest Descent. It is often redundant or inefficient when it’s close to the true solution. Can we improve somehow? For example, if we can pick $n$ orthogonal search directions {$d_1, d_2, … d_n$} such that we only need exactly one step for each direction to get to the solution, it would be much more efficient. One obvious choice (but impractical) is to choose coordinate axes as our search directions. This would lead us to:

   • Update Equation: $x_{i+1} = x_i + \alpha d_i$
   • How to find $\alpha$ :
     • Observe that $di$ has to be orthogonal to $e{i+1} = x_{i+1} - x$. So,

1. But we don’t know $e_i$ (because we don’t know $x$) so this is useless. But we can modify the above idea by picking an $A$-orthogonal set of search directions, instead of orthogonal one. $d_i$ and $d_j$ is $A$-orthogonal if $d_i^T A d_j = 0$. How can we find an appropriate step size?

2. Recall the original idea of step size: we want to minimize the function value most by choosing the best step size. It means we want to solve $argmin f(x_i + \alpha d_i)$. Setting the derivative w.r.t. $\alpha$ equal to 0 tells us that

   $\frac{\partial{f(x_{i+1})}}{\partial \alpha} = 0 \iff \nabla f(x_{i+1})^T \frac{d}{d \alpha} x_{i+1} = 0 \iff -r_{i+1}^T d_i = 0 \\$

(directional derivative: http://tutorial.math.lamar.edu/Classes/CalcIII/DirectionalDeriv.aspx)

Now recall that $r_i = b - Ax_i = b - Ax + Ax - Ax_i = -Ae_i$ (Note: b - Ax = 0). So the last term will become
$$e_{i+1}^T A d_i = 0 \iff (e_i + \alpha d_i)^T A d_i = 0 \\ \iff \alpha = -\frac{e_i^T A d_i}{d_i^T A d_i} = -\frac{r_i^T d_i}{d_i^T A d_i}$$

• So how to find an A-orthogonal set of search directions? Is the existence even guaranteed?

Gram-Schmidt Conjugation

https://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf

Consider the following Primal Problem:

Then the Lagrange function will be

$$
L(x,p) = c^T x + p^T(b-Ax)
$$

If we stare at it for a while, we notice that we can rewrite the primal problem as

(Suppose $b-Ax\ge0$. Then by letting $p$ large, we can make $\max_{p\ge0} L(x,p)$ arbitrarily large. In order to have a sensible solution, we need $b-Ax \le 0$; the constraint is implicitly incorporated by this $max$ operator.)

Flip min and max, and then you get the dual problem:

[On-going notes.]

Invention of pre-training

2006: Hinton & Salakhutdinov “Reducing the Dimensionality of Data with Neural Networks”

2007: Bengio “Greedy layer-wise training of deep networks”

Pre-training resolved the issue associated with training deep networks.

Glorot, X. and Bengio, Y. “Understanding the difficulty of training deep feedforward neural networks”

2nd order method

2010: Martens “Deep Learning via Hessian-Free optimization”

• showed that HF “is capable of training DNNs from certain random initializations without the use of pre-training, and can achieve lower errors for the various auto-encoding tasks considered (by Hinton & Salakhutdinov” (Hinton 2013))

maybe SGD wasn’t that bad to train deep nets?

• Notably, Chapelle & Erhan (2011) used the random initialization of Glorot & Bengio (2010) and SGD to train the 11-layer autoencoder of Hinton & Salakhutdinov (2006), and were able to surpass the results reported by Hinton & Salakhutdinov (2006). While these results still fall short of those reported in Martens (2010) for the same tasks, they indicate that learning deep networks is not nearly as hard as was previously believed.

Dropout

2012: Hinton [“Improving neural
networks by preventing co-adaptation of feature detectors”]
(http://arxiv.org/abs/1207.0580)

learning rate schedule for momentum

2013: Hinton “On the importance of initialization and momentum in deep learning”

• when stochastic gradient descent with momentum uses a well-designed random initialization and a particular type of slowly increasing schedule for the momentum parameter, it can train both DNNs and RNNs (on datasets with long-term dependencies) to levels of performance that were previously achievable only with Hessian-Free optimization

Interesting remark:

• Furthermore, carefully tuned momentum methods suffice for dealing with the curvature issues in deep and recurrent network training objectives without the need for sophisticated second-order methods.

-> what is the reasoning behind this?

• the optimization problem resembles an estimation one)

• One explanation is that previous theoretical analyses and practical benchmarking focused on local convergence in the stochastic setting, which is more of an estimation problem than an optimization one (Bottou & LeCun, 2004). In deep learning problems this final phase of learning is not nearly as long or important as the initial “transient phase” (Darken & Moody, 1993), where a better argument can be made for the beneficial effects of momentum.

what does this estimation-optimization thing mean?

The progress on image generation has been dramatically improved due to VAE/GAN. The quality of Figure 5 in this paper is incredible.

Links:

http://tinyclouds.org/colorize/

Notes:

• This problem, (gradient vanishing problem) however, has been largely addressed by normalized initialization [23, 9, 37, 13] and intermediate normalization layers [16], which enable networks with tens of layers to start converging for stochastic gradient descent (SGD) with backpropagation [22].

• Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error, as reported in [11, 42] and thoroughly verified by our experiments. Fig. 1 shows a typical example

Important notes:

“Thus, given the proliferation of saddle points, not local minima, in high dimensional problems, the entire theoretical justification for quasi-Newton methods, i.e. the ability to rapidly descend to the bottom of a convex local minimum, becomes less relevant in high dimensional non-convex optimization.”

The proposed algorithm uses the second order curvature information in a different way than quasi-Newton methods.

Check:

“Typical, random Gaussian error functions over N scalar variables, or dimensions, are increasingly likely to have saddle points rather than local minima as N increases. Indeed the ratio of the number of saddle points to local minima increases exponentially with the dimensionality N.”

“Second order methods, like the Newton method, are designed to rapidly descend plateaus surroudning local minima by rescaling gradient steps by the inverse eigenvalues of the Hessian matrix.” -> “H

I read an article about Viterbi algorithm on wikipedia today, which (somehow) reminded me of interesting combinatorics problems back in the day. So I will share some of my favorite ones.

Give an intuitively understandable description to the following combinatorics expressions:

I recently read the lecture notes of Stanford CS294A to learn about autoencoder, but I thought the derivation of partial derivatives for backpropagation algorithm in the lecture notes is a bit unfriendly, so I will try to fill a gap.

On page 7, he describes one iteration of gradient descent updates as follows:
$$W_{ij}^{(l)} := W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}}J\left(W,b\right)$$

We want to find the partial derivative. On the next page, he explains how the backpropagation algorithm can find partial derivatives, but he just set the error term $\delta$ out of nowhere, and it is hard to see where it actually comes from.

We’ll try to see how the error term delta appears from the gradient update equation.

So, the partial derivative in the update equation can be written as follows by chain rule:

From equation (6) on page 5 $z^{(l+1)} = W^{(l)}a^{(l)} +b^{(l)}$, we can see that the partial derivative Z/W is equal to a. So,

Now, we introduce the delta term by letting
$$\delta_i^{(l)} = \frac {\partial J\left(W,b\right)} {\partial z_{i}^{(l)}} =\frac {\partial J\left(W,b\right)} {\partial a_i^{(l)}} \frac {\partial a_i^{(l)}} {\partial z_{i}^{(l)}} = \frac {\partial J\left(W,b\right)} {\partial a_i^{(l)}} f'(z_{i}^{(l)})$$

We look at the partial derivative we get above: $\frac {\partial J\left(W,b\right)} {\partial a_i^{(l)}}$. We can expand this partial derivative by chain rule as follows:

When l = $n_l$:

Note that
$$a^{n_l} = h_{W,b}(x) \\ J(W,b) ={\frac {1} {2} \left\| y-h_{W,b}(x)\right\|^2}$$
as defined on page 6 in the lecture notes.

When l $\neq n_l$:
$$\frac {\partial J\left(W,b\right)} {\partial a_{i}^{(l)}} = \frac {\partial J\left(W,b\right)} {\partial z_{1}^{(l+1)}} \frac {\partial z_{1}^{(l+1)}} {\partial a_i^{(l)}} + \frac {\partial J\left(W,b\right)} {\partial z_{2}^{(l+1)}} \frac {\partial z_{2}^{(l+1)}} {\partial a_i^{(l)}} + ... + \frac {\partial J\left(W,b\right)} {\partial z_{s_{l+1}}^{(l+1)}} \frac {\partial z_{s_{l+1}}^{(l+1)}} {\partial a_i^{(l)}} = \sum _{j=1}^{s_{l+1}}W_{ji}^{(l)}\delta_i^{(l+1)}$$

Note that from the equation (6) in the lecture notes and as we define earlier,
$$\frac {\partial J\left(W,b\right)} {\partial z_{j}^{(l+1)}} = W_{ji}^{(l)} \\ \delta_i^{(l+1)} = \frac {\partial J\left(W,b\right)} {\partial z_{i}^{(l+1)}}$$

The idea behind the derivation for $l < n_l$ (or actually, the whole algorithm of backpropagation) is sort of similar to dynamic programming. We want to know the partial derivative $\frac {\partial J\left(W,b\right)} {\partial a_{i}^{(l)}}$. That is, we want to know how a small change in $a_i^{(l)}$ might affect the overall cost function $J(W,b)$. In order to find that, we look for the consequences in the layer right after the layer l, which is (l+1). These values in the layer l+1 have to be computed prior to the current node in the layer l, which is $a_i^{(l)}$. Indeed, these values are already computed when we compute the value for $a_i^{(l)}$ because we start with the last layer, and move backward. This is exactly the idea behind dynamic programming.

Finally, from above, we can get to the expressions as the lecture notes have on page 8 in the backpropagation algorithm:
$$\delta_i^{(n_l)} = -(y_i-a_i^{n_l})f'(z_i^{(n_l)}) \delta_i^{(l)} = \left( \sum _{j=1}^{s_{l+1}}W_{ji}^{(l)}\delta_j^{(l+1)}\right)f'(z_i^{(l)}) \frac {\partial } {\partial W_{ij}^{(l)}} J(W,b) = a_j^{(l)}\delta_i^{(l+1)}$$

Overall, the reason why the partial derivatives can be represented using the delta term is a bit hard to follow is that the logical flow of the derivation is flipped. The way the lecture notes set the delta term seems magical because it doesn’t explain why we would set the term as it is. The answer is that we just set it because that way the equations (in the derivation) look much simpler (and indeed, by setting the delta term, we can visualize filling up the 2D table, where each entry is a corresponding delta term as we do in dynamic programming.) If the delta term were introduced just for the convenience to make the equations look simpler in the sequence of computation from the update equation, it would have been much easier to follow.